数据预处理与K-means聚类实现
Report-hw1-Data Analysis and Mining
Task 1 Data pre-processing
数据集
- 数据集来源:Bank Marketing Dataset
- 数据集描述:这个数据集描述了某银行进行的最后一次营销活动,从而帮助该银行找到改进下一次营销活动的最佳策略,并确定有助于制定未来战略的模式。
- 数据集特征:
该数据集共有17列,11162行,各列属性含义如下所示:
age 年龄
job 职业(admin,unemployed,student,retired,self-employed,housemaid,services,bluecollar,technician,management,entrepreneur,unknown)
marital 婚姻状况(single,married,divorced)
education 受教育水平(primary,secondary,tertiary,tertiary)
default 是否有违约记录(yes,no)
balance 账户平均余额
housing 住房贷款
loan 个人贷款
contact 与客户联系沟通方式(cellular,telephone,unknown)
day 最后一次联系的时间
month 最后一次联系的月份
duration 最后一次联系的交流时长
campaign 与客户交流的次数
pdays 最后一次联系客户过去多久
previos 与客户交流次数
poutcome 上一次活动的结果(success,failure,unknown)
deposit 是否有定期存款(yes,no)
预处理
原数据集已被清洗的较为完整,所以该作业中人为添加了一些“脏数据”,包括缺失值,异常值等,如下图所示:
缺失值:

异常值:



异常值处理

- 首先,我们认为age也就是年龄的正常范围应该在1-100,所以先将这些正常范围的age筛出
- 对筛出来的age取均值(b.mean())
- 遍历数据集,将越界的age改为均值
- 接下来处理balance列的异常值,由于之前把几个原本的数据改为了字符串,导致了全列数据被类型转换为了字符串,所以检测异常值只需要看每个数据第一位是否是数字即可,若是,则填充为int值0,若不是,则类型转换为int
缺失值处理

缺失值处理较为简单,采用均值填充法,直接用fillna方法将均值填充进去即可
数据过滤和选择


由于聚类目的是确定优先联系进行营销的客户组别,所以我们只需要那些非管理人员(客户)、有存款、没有负债的数据,基于此,我们进行数据过滤操作;除此之外,我们只需要选择比较核心的数据特征进行聚类即可,一方面便于标准化,另一方面其余列属性的值种类太少,不便于聚类
数据标准化

数据标准化操作是将数据按比例缩放,使之落入一个小的特定区间。其中最典型的就是数据的归一化处理,即将数据统一映射到[0,1]区间上。
这里选用的标准化方法是z-score标准化,这种方法给予原始数据的均值(mean)和标准差(standard deviation)进行数据的标准化。经过处理的数据符合标准正态分布,即均值为0,标准差为1,其转化函数为:
x* = (x - μ ) / σ
其中μ为所有样本数据的均值,σ为所有样本数据的标准差。标准化后的变量值围绕0上下波动,大于0说明高于平均水平,小于0说明低于平均水平。
这里我们将数据类型为字符串的poutcome和job两列数据转化为数字索引,便于标准化。
本作业中处理后的数据形式如下所示:

Task 2 Clustering algorithms
Kmeans聚类算法的实现
实现流程如下:
- 在数据集中随机选取k个数据,作为初始质心;

- 计算数据集中每个样本到每个质心的距离,把样本划分到距离最小的质心所属的类别;
计算欧氏距离的函数:即x1与x2平方和的平方根

计算每个样本到质心的距离,并把样本划分到距离最小的质心所属的类别:这里采用字典作为数据结构,通过键值对的形式为样本划类

- 根据聚类结果,重新计算质心,当本次计算的质心与上一次质心完全一样(或者收敛)时,停止迭代;
否则更新质心,继续执行步骤1、2、3。

- 最后产生聚类结果y_preds:

算法实现的困难
- K值的选取不好把握
- 采用迭代方法,得到的结果只是局部最优。
- 把样本划分到距离最小的质心所属的类别这一步的数据结构选取上遇到了困难,一开始没有想到用字典来实现
- 停止迭代的标志一开始难以确定
算法优化
Kmeans++优化:
经过实验,发现Kmeans跑出来的聚类结果不稳定,原因是它随机选取k个数据,导致结果无法收敛。
因为随机选取,可能会使选取的几个数据点都非常靠近,不仅导致算法收敛很慢,还会导致结果只收敛到局部最小值。
所以我们使用Kmeans++的方法初始化质心进行优化,其实现流程如下:
- 从输入的数据点集合中随机选择一个点作为第一个聚类中心;

- 对于数据集中的每一个点xi,计算它与已选择的聚类中心中最近聚类中心的距离D(x);

- 选择一个新的数据点作为新的聚类中心,选择的原则是:D(x)较大的点,被选取作为聚类中心的概率较大;

- 重复2和3直到选择出k个聚类质心;

- 利用这k个质心来作为初始化质心去运行标准的K-Means算法;
n_init二次优化:
该优化即算法执行n_init次,最终结果取最优的一次(所有样本点到所属的聚类质心的距离之和最小,即为最优)
数学表现如下:
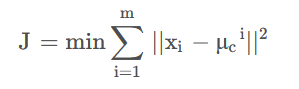
在Kmeans++方法选取质心的基础上,再添加参数n_init来优化聚类的准确性和稳定性,为此我们定义函数select_optimal:

该函数找到n_init次运行中,J最小时,对应的聚类质心,即为最优解。
k值选取方法优化:
传统的k值选取方法使用肘部图法,我们这里采用从簇内的稠密程度和簇间的离散程度来评估聚类的效果。常见的
方法有轮廓系数Silhouette Coefficient和Calinski-Harabasz Index。
这里我们使用sklearn中已封装好的sklearn.metrics.calinski_harabasz_score方法来选取k值
它的得分越高,聚类效果越好,得分最高时,就是最佳的k值。
具体过程如下:
k=5:
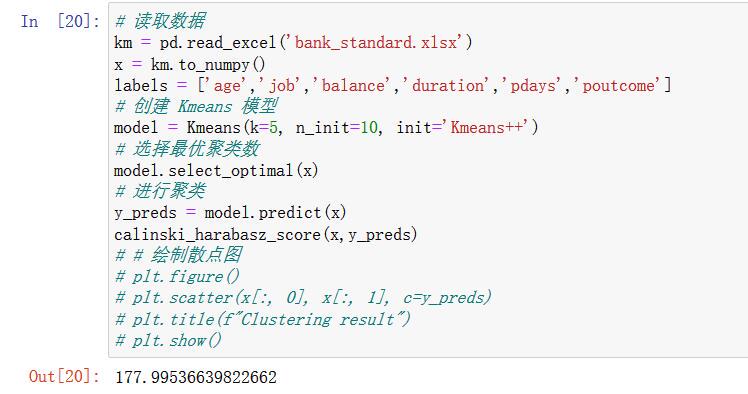
k=6:
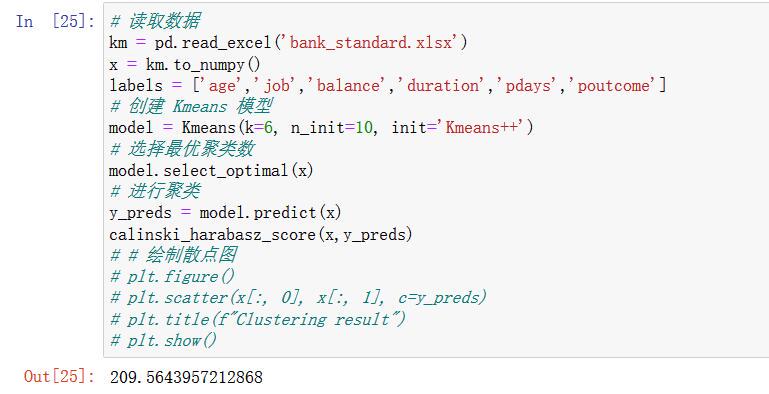
k=7:
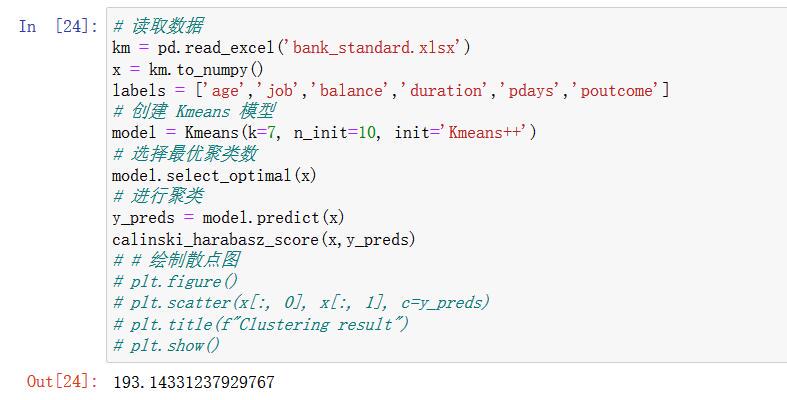
可以看到,K=6的时候,得分最高,6就是我们要找的k值。
实验结果及比较分析
结果展现绘图
结果展现形式:散点图
由于我们的数据是6维的,要绘制散点图需要进行降维,这里我们采用PCA法(主成分分析)降到二维:

传统Kmeans聚类结果
在自主实现的Kmeans类中,我们指定init参数为random即可实现传统Kmeans聚类
第一次聚类:
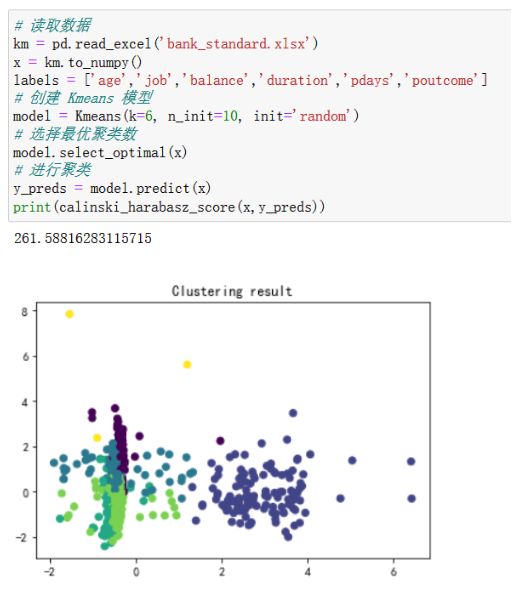
第二次聚类:
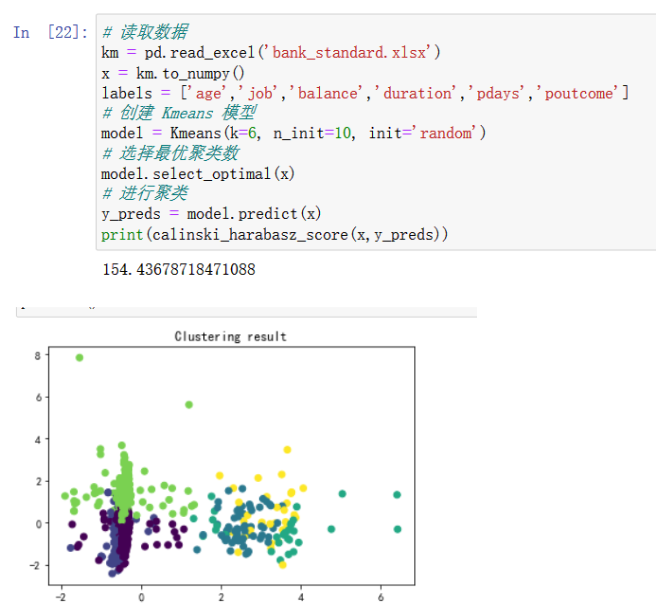
第三次聚类
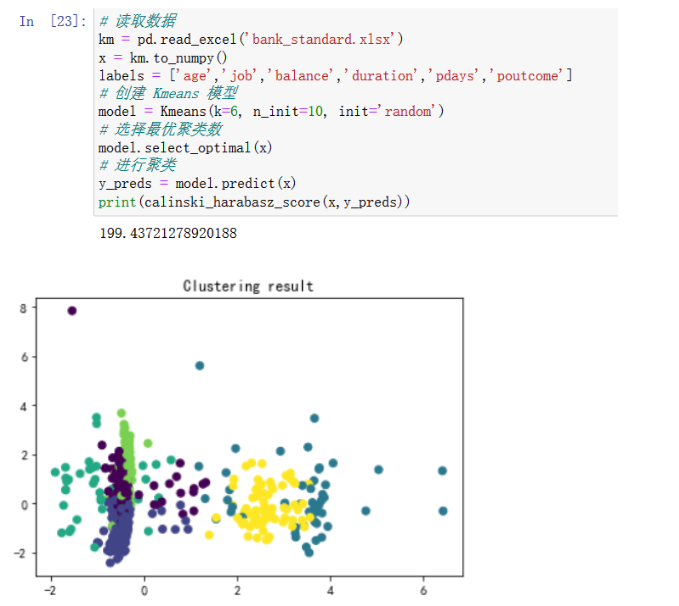
从calinski_harabasz_score得分和散点图可以看出,每次聚类的效果都不一致,这说明传统Kmeans的聚类很不稳定
优化算法聚类结果
在自主实现的Kmeans类中,我们指定init参数为Kmeans++即可实现传统Kmenas聚类
第一次聚类:
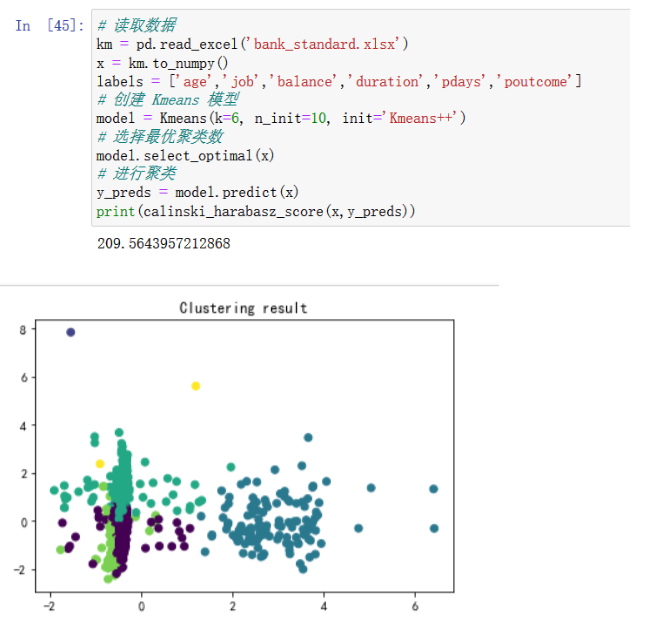
第二次聚类
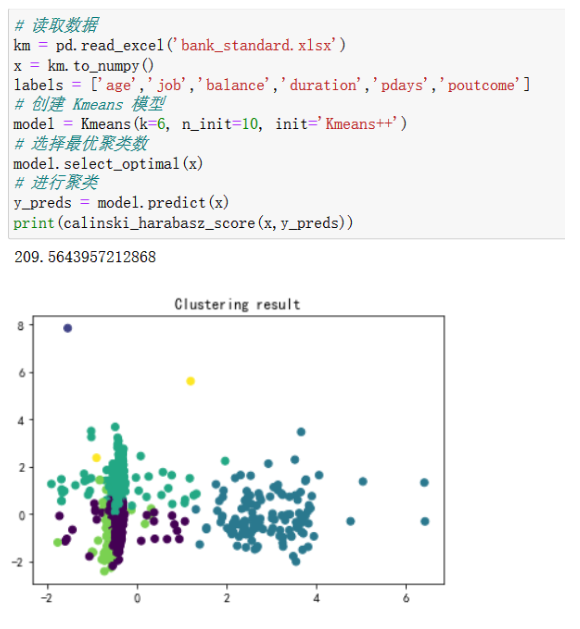
第三次聚类
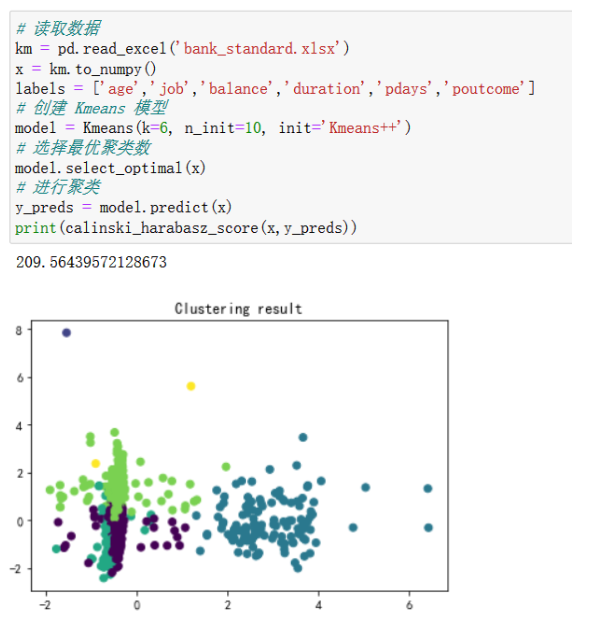
不难看出,相比于传统Kmeans方法,我们的优化算法聚类效果稳定的多,且从calinski_harabasz_score得分可以看出,优化算法的平均聚类效果更好。